

The sextant is the preferred instrument for measuring those angles, which are measured in the units: degrees, and minutes. The position of celestial bodies and other points on the surface of the earth can be defined and located by a description of angles. In mathematics, an orientation on a real vector space is a choice of which ordered bases are "positively" oriented (or right-handed) and which are "negatively" oriented (or left-handed).Īngles are the most common type of numbers that astronavigators and celestial navigators calculate. This relation holds true whether the Earth is approximated as a perfect sphere or as a reference ellipsoid. If the coordinates (longitude and latitude) of a point on the Earth's surface are (Θ, Φ), then the coordinates of the antipodal point can be written as (Θ ± 180°,−Φ).
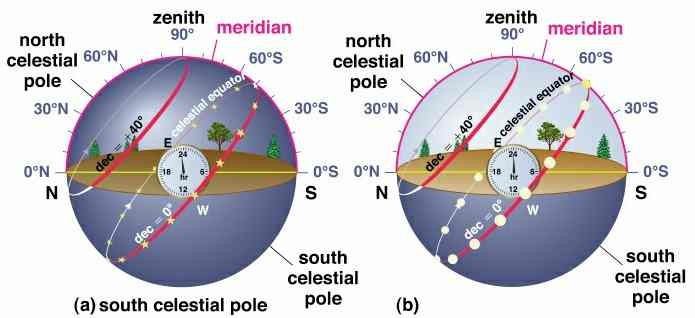


Locally, the projective plane has all the properties of spherical geometry, but it has different global properties. Contrast this with hyperbolic geometry, in which a line has two parallels, and an infinite number of ultra-parallels, through a given point.Īn important geometry related to that modeled by the sphere is called the real projective plane it is obtained by identifying antipodes (pairs of opposite points) on the sphere. Spherical geometry is the simplest model of elliptic geometry, in which a line has no parallels through a given point. In spherical geometry angles are defined between great circles, resulting in a spherical trigonometry that differs from ordinary trigonometry in many respects, including that the sum of the interior angles of a triangle exceeds 180 degrees. On the sphere the geodesics are the great circles, so the other geometric concepts are defined like in plane geometry but with lines replaced by great circles. In plane geometry the basic concepts are points and line, whereas on the sphere points are similarly defined and the equivalents of lines are differently defined as "the shortest paths between points," which is called a geodesic. Spherical geometry, the geometry of the two-dimensional surface of a sphere, is an example of a non-Euclidean geometry and has important practical uses in navigation and astronomy. Mathematical models of Algebra, Calculus, Geometry, and Trigonometry that explore astronavigation. Navigational angles between the horizon and selected celestial objects are used to locate a position on the globe and those angles translate directly to the mathematical models of Algebra, Calculus, Geometry, and Trigonometry of my assignments and within the latest New Haven Math Curriculum. Add the mistake of the index measured before or after the measurement = Add the constant misconception of the sextant from the certificate = If the center half was used, add that time starting from the center half. Greenwich Hour Angle and Local Hour Angle comparisons.Ĭorrect the deciphered value on the chronometer according to these principles: Greenwich Hour Angle - (from the Nautical Almanac). declination (from the 'Nautical Almanac').


 0 kommentar(er)
0 kommentar(er)
